The Delphi model
We model abstract concepts such as food security and conflict as real-valued latent variables, and indicators corresponding to these concepts as observed variables. An indicator is a measurable quantity that correlates with the intuitive, natural language interpretation of the abstract concept. For example, average dietary energy supply adequacy is one among many indicators for the concept of food security.
We interpret sentences such as “A small increase in conflict causes a large decrease in food security.” as saying something about the functional relationship between two latent variables representing conflict and food security respectively - that is, the sentence is giving us a clue about the shape of \(\frac{∂(\text{food security})}{∂(\text{conflict})}\)
To convert a sentence like the one above to a dynamic Bayes network, we first construct latent states composed of the variables and their partial derivatives with respect to time. In our model, the transition function that tells us how to calculate the latent state at a time step given the latent state at the previous time step is itself a random variable, with a probability distribution constructed from Gaussian kernel density estimators of empirical, crowdsourced data about how humans quantitatively interpret gradable adjectives such as small and large. The reason for this is that there is a great deal of uncertainty in the model itself, since there is no precise model for many abstract concepts such as food security and conflict that we expect to encounter in machine reading. Finally, we use the following emission model - let \(n_{ij}\) be the value of the \(j^{th}\) indicator for the \(i^{th}\) component of a latent state vector \(\mathbf{s}\). We then define probability distribution for the value of the indicator as
where \(\mu_{ij}, \sigma_{ij}\) are the mean and standard deviation of the indicator \(n_{ij}\). The structure of the model is shown in the figure below.
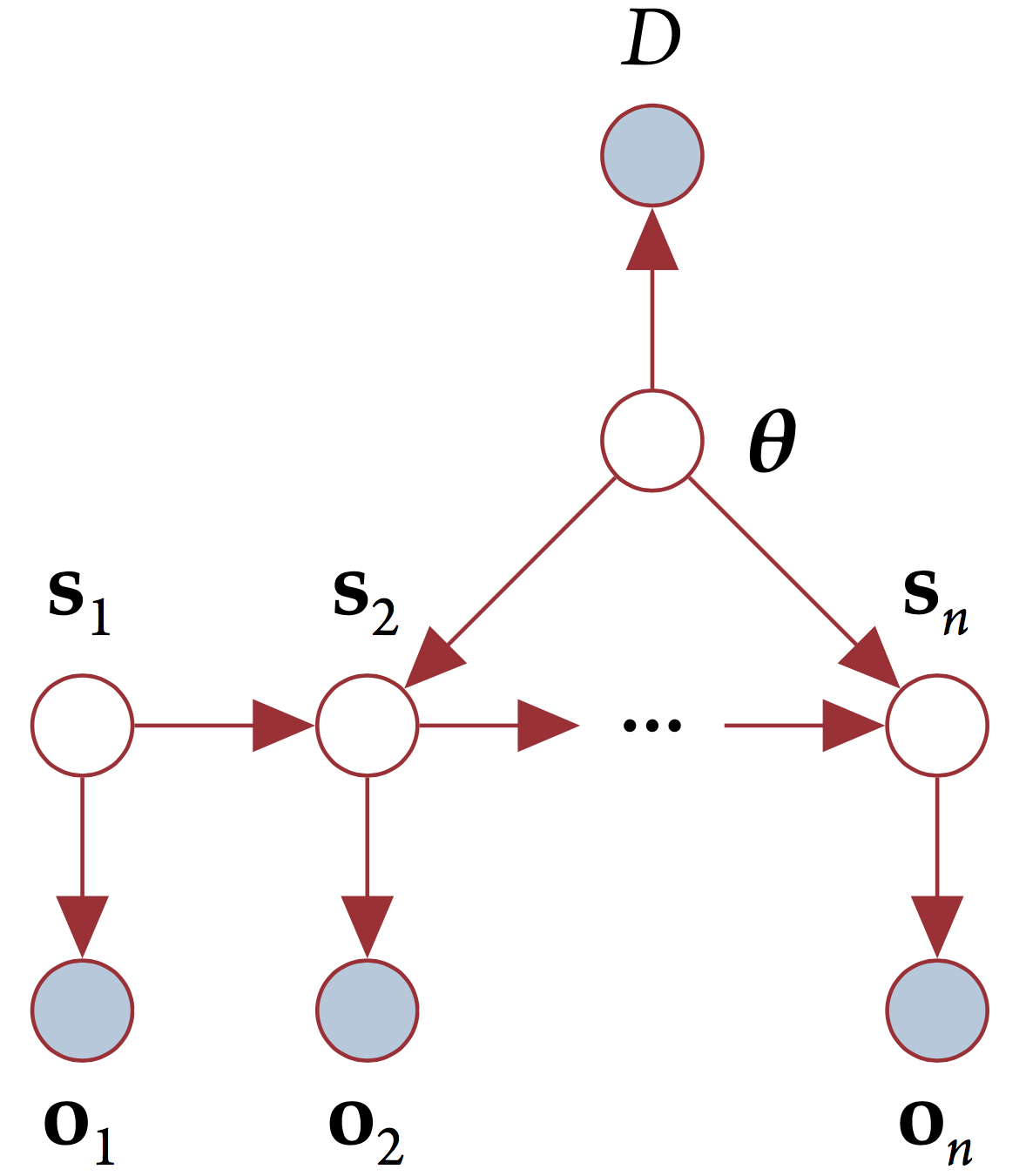
The figure depicts the model that underlies Delphi - a linear dynamical system with a stochastic transition function. The nodes \(\mathbf{s}_n\) are latent state vectors, \(\mathbf{\theta}\) is the transition model, and \(D\) represents evidence from machine reading.
For more details on the model construction, see this document.