Month 9 Milestone Report

Link to the PDF version of this report.

Overview

This report summarizes progress towards AutoMATES milestones at the nine month mark, emphasizing changes since the m7 report.

Work this phase has focused on perparations for the September demo, in collaboration with GTRI and Galois.

Highights:

• Program Analysis haindling GOTO statements, representing floating point precision, and handling of some lexical differences between Fortran dialects
• Summary of current DSSAT code coverage (in Program Analysis section); key highlight: of 162,290 lines of source code in DSSAT, PA can now handle 144,370, or 89%.
• Work on the general information source grounding/linking task: how we association source code elements (identifiers), equation terms and concepts expressed in text (both in comments and documentation). We have initial methods for linking some elements, with focus on linking equation terms to document text elements.
• Text Reading progress on extracting variable value unit information from text.
• Equation Reading has full implementation the im2markup model for extracting equation latex from images and has compiled a corpus of 1.1M equation examples. Team now working on data augmentation to improve equation extraction generalization.
• Model Analysis has developed an algorithm for variable value domain constraint propagation, identifying the possible intervals of values that can be computed given the source code representation.

Updates to GrFN

Link to the month 9 report release version (v0.1.m9) of the GrFN specification.

During this phase there were modest changes to the GrFN spec, with the main work on GrFN coming in the form of planning for converting the GrFN specification to OpenAPI schema. The new version will be released with the month 11 report.

The following are changes made to GrFN this phase:

• The introduction of identifiers, including <identifier_spec>, <identifier_string> and <gensym> (to denote identifiers in generated code)
• Revised the introduction to reflect the new changes and clarify some topics.
• Updates to naming conventions for variables and functions
• General cleanup of discussion throughout.

Program Analysis

Constructs

The work on Program Analysis has focused on extending the set of Fortran language constructs that can be handled, focusing in particular on constructs that do not have straightforward analogues in our intermediate representation (IR) languages of Python and GrFN. The following issues were a significant component of our efforts during this reporting period:

1. GOTO statements. These are common in legacy Fortran code and occur in many places in the DSSAT code base. Our approach to handling this construct is to eliminate GOTO statements by transforming the program’s abstract syntax tree (AST) using techniques described in the paper “Taming Control Flow: A Structured Approach to Eliminating Goto Statements”, by A. M. Erosa et al., Proceedings of 1994 IEEE International Conference on Computer Languages (ICCL’94), IEEE.

2. Floating-point precision. Fortran uses single-precision floating point values by default, while Python uses double-precision values. While seemingly trivial, this difference can result in profound behavioral differences between a Fortran program and a naively-translated Python version of that code. In order to preserve fidelity with the original models, we implemented a floating-point module in Python that faithfully models the behavior of Fortran floating-point computations and also explicitly represent associated precision within the GrFN representation.

3. Lexical differences between Fortran dialects. While expanding the set of source files handled, we encountered Fortran modules written in different dialects of Fortran, with different lexical rules (e.g., continuation lines are written differently in Fortran-90 than in Fortran-77). These differences have to be handled individually, which can be time-consuming. However, it gives us the ability to parse multiple dialects of the language and thereby broaden the programs we can handle.

In addition to these items, we also worked on handling a number of other language constructs in Fortran, including derived types and SAVE statements.

DSSAT Code Coverage

The following is an estimate of the number of lines of code in the DSSAT code base that can be handled by the parsing components of Program Analysis. (Not all of this can yet be translated to GrFN.) The DSSAT code base consists of the 162,290 lines of Fortran source code in 669 source files (not counting comments, which we handle separately). Program Analysis parsing can now cover 144,370 lines, which works out to a coverage of 89.0%. An analysis of the constructs that are currently not handled shows two conclusions:

1. The number of remaining unhandled language constructs is not very large: 22 keywords.

2. A small number specific coding patterns, e.g., the mixing of single- and double-quotes in strings, together account for a large fraction of the remaining unhandled lines (i.e., other than the unhandled language constructs mentioned above). The issues raised do not seem to be particularly difficult technically, and we expect to address them as we work down our prioritized list of goals.

Linking

General Linking Problem

A very important part of the AutoMATES architecture is the process for grounding code identifiers (e.g., variables) and equation terms to scientific concepts expressed in text. Ideally, identifiers, equation terms and concepts expressed in text are eventually linked to domain ontologies. However, there is great value in linking these elements even if they cannot be grounded to an existing ontology. We conceptualize the grounding task as the assembly of a network of hypothesized association links between these elements, where each link expresses the hypothesis that the linked elements are about the same concept.

This phase we further explored our conception of the overall grounding task, in terms of the types of links between information source elements, and this is summarized in the figure.

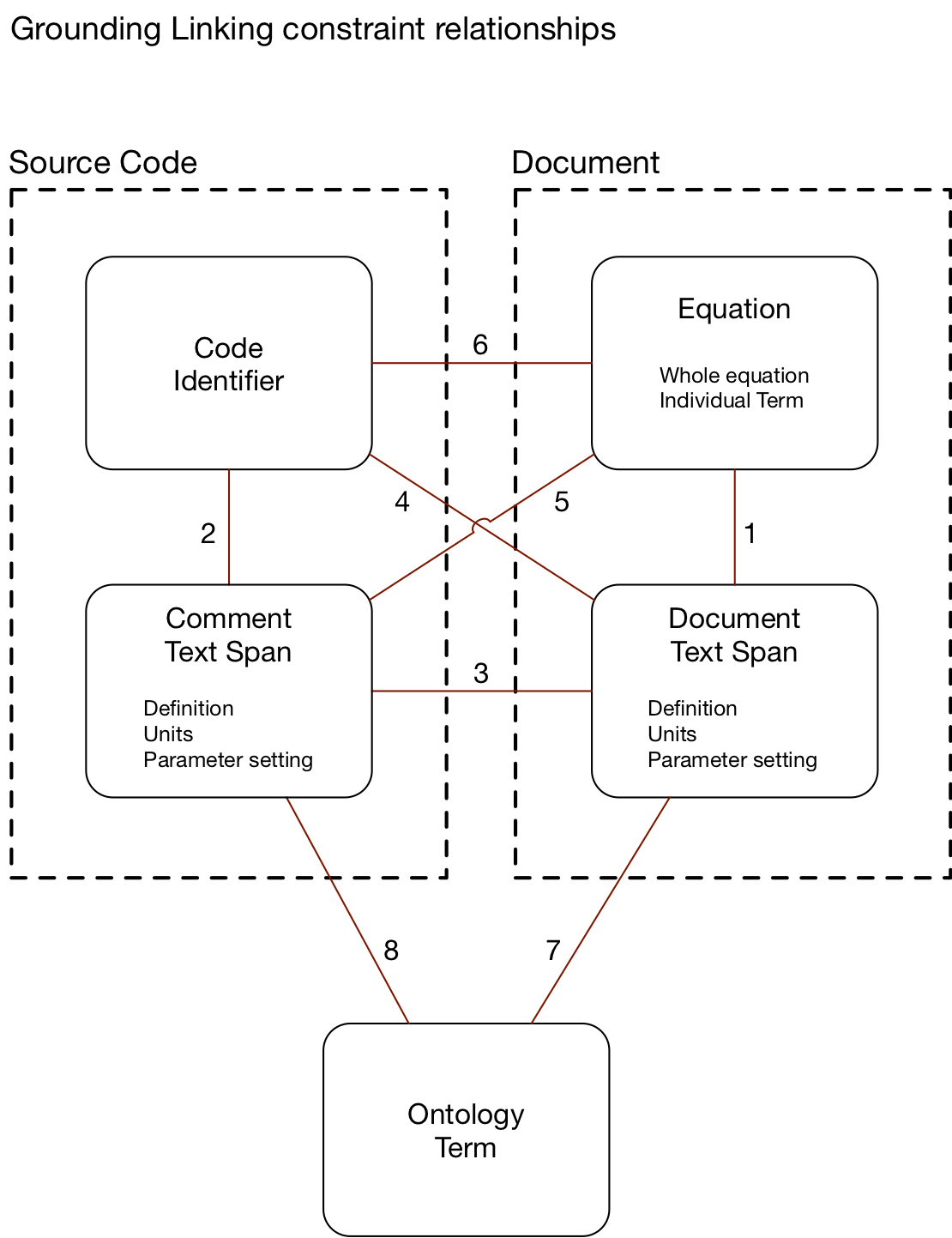
There are four types of information source element types, coming from two sources:

• Source code, which include
  • Code Identifiers
  • Code Comments
• Documents, which include
  • Document text
  • Equations

Code comments and document text in turn express at least three kinds of information:

• Descriptions (defintiions): associating a term with an expression, definition or definition of a concept.
• Units: associating the scale or units of a quantity.
• Parameter setting: expressing value constraints or specific values associated with a quantity.

Each link between source element types is made by a different inference process that depends on the information available in the sources.

• Link type 1 involves associating equations and their component terms to concepts in text. The start of our approach to identifying these links is described in the next section.
• Link type 2 involves associating code identifiers with concepts expressed in source code comments. In this phase, we infer these links by identifying mentions of the identifier names in source code text. In the future we will also make use of proximity of comments to locations in code as well as code scope to additionally support identifier-to-comment associations.
• Link type 3 involves associating code comment and document text. This linking inference is performed using a similarity score based on text embedding distance.
• Link types 4, 5 and 6 are mapped out here, but we do not yet provide inference methods for these.
• Link types 7 and 8 involve mapping textual mentions of concepts to terms in one or more domain ontologies. We are working with Galois to demonstrate this in the September demo. The core approach will likely be an embedding similarity scoring, similar to the approach to Link type 3.

Text and Equation Linking

The team is working to not only extract variables from equations, but also to link them to the in-text variables as well as the source code variables. In order to evaluate the performance of the former, the team has begun creating an evaluation dataset. The specific task the team is looking to evaluate is linking the equation variables to their in-text definitions (ex. 1) and, when present, the associated units (ex. 2).

This effort will include the following steps:

• (in progress) collecting the documents to annotate: currently, the team is working on creating a set of heuristics to select the documents most suitable for the annotation exercise;
• (in progress) creating the annotation guidelines: the team is going through an iterative process of testing the guidelines on a small number of annotators and adjusting the guidelines based on the quality of elicited annotations, the level of agreement between the annotators, and the annotators’ feedback;
• annotating the documents;
• calculating the inter-annotator agreement score as a measure of quality of the created dataset.

Once completed, the team will use the collected dataset to evaluate linking techniques.

Text Reading

The team has been working on improving the quality of the extraction of variable units from text and comments.

Extracting units from text:

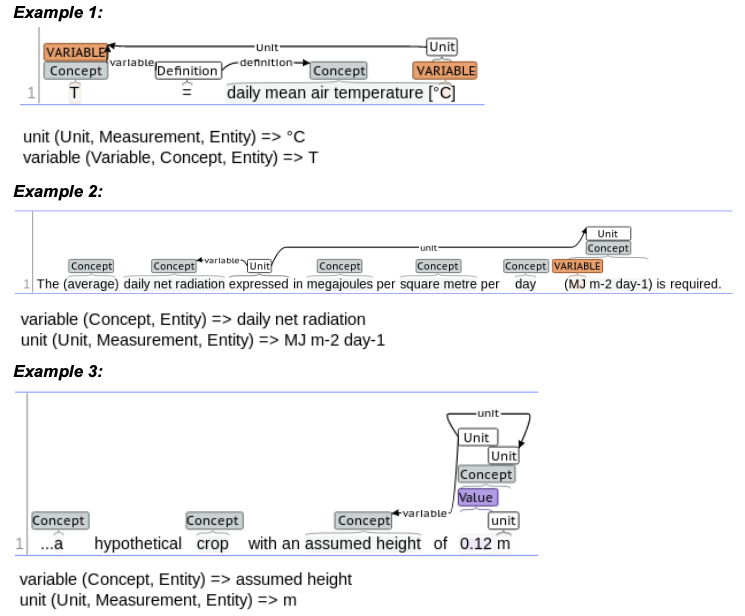
Figure 1: Example of units in text.

Extracting units from scientific text (see examples above) is a multi-step process. First, a number of basic units are extracted with a lexicon-based entity finder; the lexicon has been recently updated to exclude a number of basic units that resulted in false positives due to their similarity to variables. Second, composite (i.e., multi-token) units as well as units which are not in the lexicon, are extracted using rules. False positives are eliminated by applying a set of heuristic constraints (e.g., number of tokens in the candidate unit, length of each token in the candidate unit, presence of digits, etc.). Finally, units are attached to the relevant previously-found variables (ex. 1) and concepts (exs. 2-3) with rules. Frequently, units occur in sentences that do not include the relevant variable, with units attaching to the variable definitions/concepts. To address this issue, the team will start working on resolving these definitions/concepts to the relevant variables in the surrounding text.

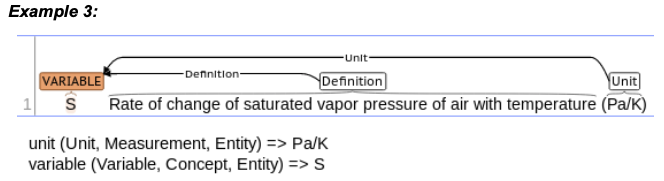
Figure 1: Example of units in comment.

With comments being less varied than text, extracting units from comments happens in only two stages: extracting units with a rule and attaching the unit to the previously found variable with another rule (see example above).

Equation Reading

Now that the team has a fully working implementation of the im2markup model, they have formatted and normalized data from one year of arxiv to use for training. This amounts to over 1.1M equation examples, an order of magnitude more training data than was used in the original and the newly gathered data represents a wide variety of domains (as compared to the original data which was only from particle physics). The team is currently training a model on this larger dataset.

Additionally, the team is working on data augmentation, as previously mentioned, and to complement that effort, they are beginning to implement the Spatial Transformer Network (STN; Jaderberg et al., 2015). The STN is a differentiable module which learns to predict a spatial transformation for each image independently, in order to make the model as a whole invariant to any affine image tranformation, including translation, scaling, rotation, and shearing. One advantage of the STN is that it is trained end-to-end with the rest of the model, not requiring direct supervision. Instead it will learn to transform the image in such a way that the end task performance improves.

Jaderberg, M., Simonyan, K., & Zisserman, A. (2015). Spatial transformer networks. In Advances in neural information processing systems (pp. 2017-2025).

Model Analysis

Domain Constraint Propagation

Task Overview

The overall goal of the domain constraint propagation task is to find the minimum functional bounds on each of the inputs for a GrFN such that no set of input values will fail to evaluate due to a mathematical error. Concretely, minimal functional bounds are bounds that arise upon the inputs to a given computation because of the functions computed in the course of that computation. An example of this would be the arcsine function, whose domain is [-1, 1]. If the following function were present in source code, y = arcsine(x) then a constraint would be placed on the domain of x such that it would be [-1, 1] at most. In general, programs extracted from the Program Analysis team are likely to have complex interactions between variables and mathematical operations that lead to domain constraints. This means that the domain constraints of a single variable are likely going to be in terms of the other variables. This means that solutions to our domain constraint propagation problem will likely be in the form of a constraint satisfaction problem (CSP) with variables that have infinite domains. Normally time complexity is a concern for CSP problems even upon finite domains; however, those time constraints are associated with determining if the set of constraints has a solution. Our intended use case for this is as a recognizer for whether a set of input values will cause a mathematical error in calculation, so we need not worry about the widely studied time complexity concerns associated with CSPs.

The following are all true about domain constraints derived from the computations found in source code:

1. Some mathematical functions set domain constraints upon the variables in their child structures.
2. Some mathematical functions translate domain constraints upon the variables in their child structures.
3. Some mathematical functions create complex multi-interval domain constraints.
4. Conditional evaluations introduce multiple possible domain constraints over for a variable

From fact 1 items we see that the domain constraint for a particular variable will be set by mathematical functions that impose constraints on their inputs, such as arccosine and the logarithm function. These constraints will be in the form of mathematical domain intervals. Other operators will shift or scale the domain constraints intervals upon a variable, such as the addition, multiplication, and exponentiation operators. Fact 3 shows us that a particular variables domain could be a series of intervals. This can occur due to functions that impose domains with holes, such as the division operation. Now a domain constraint upon a variable can be described as a list of domain intervals for an input variable over which the output can be computed. But, as mentioned by fact 4, the presence of conditionals adds complications to the domain constraints for a variable. Now the domain constraint must be based on the conditional evaluation in cases where two separate mathematical functions make use of a variable in a constrained manner as governed by a conditional. Since our plan is to use the domain constraints discovered during the propagation process to validate input sets, we will use the most restrictive case for conditionals which will be to require any variable domains found under conditionals to fulfill the constraints of all branches of the conditional.

Algorithmic Solver Approach

Our approach to solving the domain constraint propagation problem will be to create an algorithmic solver that uses the structure of the source code that we extract our models from in order to create a graph of the constraints upon the domains of different variables. The algorithmic solver will perform a line-by-line walk through the code, and will perform a tree-walk at each line of the code, generating and updating variable constraints upon visiting operators on each line. To visualized the tree-walk that will occur for each line of code, consider the example complex mathematical equation shown below.

a = arccosine(logarithm((x*y)/5)) * square_root(z)

This can be rewritten in the following form with only one mathematical operation per-line to show how a tree-walk will occur:

(1) n0 = x * y
(2) n1 = n0 / 5
(3) n2 = logarithm(n1)
(4) n3 = arccosine(n2)
(5) n4 = square_root(z)
(6) a = n3 * n4

If we evaluate, in a similar manner as the tree-walk will occur, from line 6 backwards to line 1 we can see how the domain constraints will propagate to the input variables, such as how the domain constraint introduced by arccosine is propagated from n2 --> n1 --> n0 --> x & y. Just as this process has been carried out for a single line mathematical function, the same tree-walk can be done across lines to propagate variable constraints backwards to all the input variables of a scientific model. Using this method works very well for straight-line code; however there are atleast two questions that still need to be answered:

1. How will this method work for function calls?
2. How does this method handle loops?

For problem 1, if we can observe the code for a function call then we can treat the function exactly the same as we would straight-line code. If we cannot observe the code for a function call, but we do know it’s domain/range then we can treat this function just like any other mathematical operator upon its inputs and outputs. However, if we cannot observe the functions code and we do not have any information of its inputs or outputs then we will be unable to determine the validity of solutions to the domain constraint problem. For problem 2, if we know the number of times we are expected to loop then we can guarantee whether input sets satisfy the domain constraints; otherwise, we can perform this analysis on the loop as though it is straight-line code with a conditional.