Month 3 Report: Description of Prototype System

01 Feb 2019

Overview

In this report the AutoMATES team describes the development work done in the past two months on the AutoMATES prototype system. No changes have been made to the overall architecture design, but significant progress has been made in each of the architecture components introduced in the Month 1 Report. We are on track for successfully achieving our Phase 1 goals for the prototype.

Among the highlights for this phase, detailed in the sections below, are the following:

Deployment of a demonstration web application of the program analysis-to-function network translation translation.
Extension of the GrFN representation to represent namespaces in identifiers, for handling multi-file and multi-module systems.
Extensions of the Fortran program analysis module for handling Fortran I/O, Modules, open-ended loops, and arrays.
Development of the text reading pipeline for converting PDFs to text, extracting quantities and their domains, and a start to developing grammars for extracting variables and associating them with values.
Development of the equation detection and parsing pipeline as well as collecting the enormous arXiv PDF and TeX source corpus.
Development of an algorithm to identify structural overlap between two models, through the identification of the Forward Influence Blanket.
Improving the code summarization training corpus by expanding it dramatically, as well as progress in improving the embedding model for code summary generation.

All code supporting the contributions reported here are available in the AutoMATES and Delphi Github repositories.

Demo Webapp

A demo of the current version of the prototype system is now live - you can try it out here!

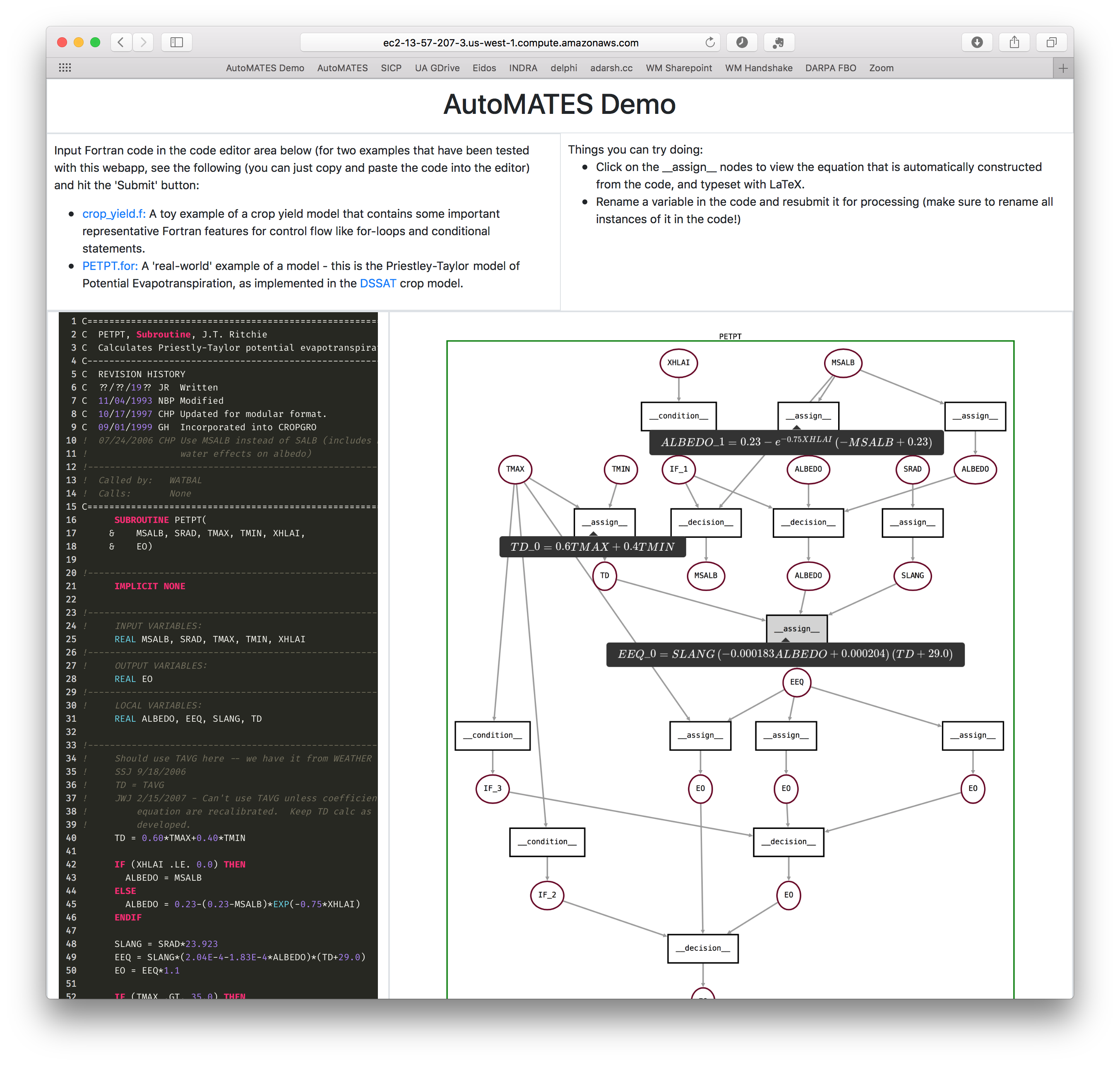
Screenshot of AutoMATES demo webapp

Figure 1: Screenshot of AutoMATES demo webapp

When Fortran source code is submitted to the demo, it is processed by the Program Analysis (for2py) pipeline, generating both (1) equivalent target executable Python internal representation and (2) matching GrFN specification representation. The GrFN specification is then rendered as a function network graph that you can interact with.

Currently, the demo has been only been tested with a limited number of programs, so we encourage users as of now to experiment by modifying the two suggested examples on the page, rather than trying to process arbitrary Fortran programs.

Clicking on the __assign__ nodes in the rendered GrFN function network graph yields a LaTeX representation of the equation corresponding to the assign statement. This equation is constructed from the Python source represented using SymPy, and will facilitate the linkage to equations extracted from papers using the equation parsing module.

For example, the screenshot above shows the analysis of the Priestley-Taylor method of calculating potential evapotranspiration, as implemented in DSSAT. Three of the __assign__ functions have been clicked, showing tooltips with black backgrounds containing some of the equations involved in this calculation - these very equations can be found on page 46 of the book Understanding Options for Agricultural Production (reproduced below - the equations matching the ones in the screenshot of the webapp are highlighted with maroon borders).

Page 46 of the book Understanding Options for Agricultural
Production

Figure 2: Page 46 of the book Understanding Options for Agricultural Production, describing the Priestley-Taylor method of calculating potential evapotranspiration.

GrFN Specification

During this phase, significant extensions were made to the GrFN specification that serves as the central representation between program analysis (which extracts variables and the network of functions among them) and model analysis (where the variables and their functional relationships are treated generally as a probabilistic dynamic systems model). The extensions include the following.

Identifiers

Prior to this update, a variety of naming conventions were used to represent source code identifiers (names for program entities such as variables, constants, functions, etc.), and the disambiguating context in which they are defined. Identifiers now systematically represent namespaces and program scope as part of their definition, along with their base name. The representation of identifiers includes the following additions and advantages:

<identifier_spec> declarations in GrFN associate identifier usage, such as the location within source code of where the identifier was declared, as well as "aliases" (other names used to refer to the same program elements). The location of identifier use will be used to connect identifiers with source code comments and documentation strings. Also, base names, aliases, and namespaces will be used as evidence for grounding variables to model domain concepts.
Inclusion of namespace and scope context in identifier definitions make it possible for program analysis to represent the context of Fortran program Modules. This context also provides a consistent method for extending source code analysis beyond single source code files.
An <identifier string> provides a single human-readable instance of an identifier while consistently representing all of its definitional information: namespace, scope, and base name. These will be used to denote instances of identifiers used in generated GrFN JSON (outside of the identifier declaration specs). For example,
```
  "CROP_YIELD::UPDATE_EST.loop$1::YIELD_EST"
```

is an identifier for a variable name originally given as "YIELD_EST" in source code, but defined in the "CROP_YIELD" namespace, and within the first loop of the function "UPDATE_EST".

Since identifiers themselves are now defined in terms of structured information (namespace, scope, and base name), identifier <gensym>s have been introduced to be used as unambiguous standins for identifiers used in generated intermediate target Python code.

Variable and Function Naming Conventions

The new systematic representation of namespace and scope rules for identifiers made it possible to clean up some of the previous ad-hoc approaches to naming variables and functions. New naming conventions have been introduced.

Conditions

The approach to representing program conditions (i.e., "if statements") was also updated. When program analysis analyzes a conditional in source code, a "condition" assignment function is introduced that sets the state of a variable representing the condition, and then one or more "decision" assignment functions are introduce that represent updates to other variables depending on the outcome of the condition.

Specification Links

Finally, there was a significant rewrite of the specification introduction as well as updates throughout to improve readability and ensure consistency.

The release version of the GrFN specification as of this report is linked here GrFN Specification Version 0.1.m3. (For the latest development version, see the Delphi docs.)

Program Analysis: for2py

Our work in for2py has focused on extending the range of Fortran language constructs handled. We have implemented support for the Fortran language constructs listed below. In addition, we have mapped out the translation of a number of additional Fortran language constructs and are currently in the process of implementing their translation.

Fortran I/O

Fortran’s file and formatted I/O handling mechanisms have been implemented in for2py so that the pipeline now generates functionally equivalent Python intermediate representation. This gives us a way to validate the front-end translation by comparing the observable behavior of the generated Python code with that of the original Fortran code. In particular, we have implemented the following:

File Input: Reading data in from a file. Analogous to Python’s read_line.
File Output: Writing data to a file in the disk. Analogous to Python’s write.
List-Directed Output: Analogous to Python’s sys.stdout.

Fortran Modules

Fortran Modules provide a mechanism for programmers to organize their code, control visibility of names, and allow code reuse; they are used extensively in DSSAT as well as other scientific code bases. We have implemented the conversion of Fortran modules to the for2py intermediate representation, and validated the translation by confirming that the resulting Python code has the same behavior as the original Fortran code.

Our implementation translates each Fortran module into its own Python file (named as m_<module_name>.py). This has a number of advantages, among them that it is easy to identify, isolate, and access the Python code corresponding to each Fortran module, and also that the Fortran module does not have to be analyzed and translated to Python more than once. Since Python does not have an explicit private command to limit the visibility of names outside a given scope, we use Python’s name mangling to replicate the behavior of Fortran’s PRIVATE declarations.

We are currently working on implementing the translation of Fortran modules from for2py intermediate representation into the GrFN specification language, where we will make use of the new identifier and naming conventions.

Open-ended Loops

for2py is able to translate Fortran DO-WHILE loops into an equivalent Python intermediate represetnation. We are currently working on implementing the translation of such open-ended loops into the GrFN specification language.

Arrays

Fortran arrays differ from Python lists in a number of ways. By default, Fortran arrays are 1-based, i.e., the first element is at index 1, while Python lists are 0-based. Fortran arrays can be declared to have lower bounds different from the default value of 1; this is not true of Python lists, which always start with index 0. Fortran arrays can be multi-dimensional, while Python lists themselves are one-dimensional. Finally, Fortran arrays support operations, such as array constructors, various sub-array manipulations, array-to-array assignments, etc., that do not have ready analogs in Python. We have implemented a library that implements Python objects that support Fortran-like array operations. Based on this library, we are currently able to translate a wide range of Fortran array constructs into the for2py intermediate representation. In particular, we can handle the following Fortran array features: single- and multidimensional arrays; implicit and explicit array bounds; and read and write accesses to arrays.

We are currently working on implementing the translation of Fortran arrays from for2py intermediate representation into the GrFN specification language.

Text Reading

Converting PDF to text

As discussed in the previous report, the first task required to perform automated text reading and information extraction was the conversion of the source documents from PDF to text. This phase the team evaluated several tools on the specific types of documents that are used here (i.e., scientific papers) and in the end the team chose to use science parse for both its quick processing of texts as well as the fact that it does a good job handling section divisions and greek letters. The team integrated science parse into the text reading pipeline via a Docker container such that it can be run offline (as a preprocessing step) or online during the extraction.

Extracting quantities

The team is also utilzing another open-source tool, grobid-quantities, which can find and normalize quantities and their units, and even detect the type of the quantities, e.g., mass. The tool finds both single quantities and intervals, with differing degrees of accuracy. The grobid-quantities server is run through Docker and the AutoMATES extraction system converts the extractions into mentions for use in later rules (i.e., the team’s extraction rules can look for a previously found quantity and attach it to a variable). While grobid-quantities has allowed the team to begin extracting model information more quickly, there are limitations to the tool, such as unreliable handling of unicode and inconsistent intervals. The team has opened several issues on the Github page for grobid-quanities and will continue to do so. If nesessary, the extraction of quantities may be moved into the Odin grammars for full control.

Rule-based extraction framework

In terms of extraction, the team has begun implementing a light-weight information extraction framework for use in the ASKE program. The system incorporates elements of Eidos (e.g., the webapp for visualizing extractions, entity finders based on syntax and the results of grobid-quantities, and the expansion of entities that participate in relevant events) along with new Odin grammars for identifying, quantifying, and defining variables, as shown here:

A screenshot of the web-based visualizer showing the results of
the rule-based extraction framework.

Figure 3: A screenshot of the web-based visualizer showing the results of the rule-based extraction framework.

This project is fully open-source and has already been utilized and contributed to by the Georgia Tech ASKE team.

To promote rapid grammar development, the team has developed a framework for writing unit tests to assess the extraction coverage. Currently, there are 77 tests written to test the extraction of variables, definitions, and setting of parameter values, of which 16 pass. This test-driven approach (in which we first write the tests based on the desired functionality and then work to ensure they pass) will allow for quickly increasing rule coverage while ensuring that previous results are maintained.

Next Steps

The immediate next steps for machine reading are to expand the coverage of the rules for natural language text and then to begin extracting information about variables from source code comments. The team will then create an end-to-end alignment tool to map variables found in code to the corresponding variable described in natural language.

Equation Detection and Parsing

ArXiv bulk download

The team has downloaded the complete set of arXiv PDFs and their corresponding source files from Amazon S3 as described here. These will be used for training and evaluating equation detection and parsing.

Preprocessing pipeline

The team has put together a preprocessing pipeline with the purpose of preparing the data for training the statistical models for equation detection.

First, the source files retrieved from arXiv are arranged in a directory structure where the first directory corresponds to the year and month of the paper submission (e.g.,1810 corresponds to October 2018). Inside, each paper’s source files are stored in a directory named after the paper’s id (e.g., 1810.04805).

Then, the file that has the \documentclass directive is selected as the main TeX file (see here for more information). Once a main TeX file has been selected, the TeX source is tokenized and the content of certain environments are collected together with the environment itself (e.g., the tokens inside the \begin{equation} and \end{equation} directives, together with the label equation).

Currently, the team is focused on processing the TeX code extracted from the equation environment, while still collecting the code from other math environments for later use.

The extracted code for each equation is rendered into a standalone equation image, and then the PDF file for the entire paper is scanned for this standalone image using template matching. The resulting axis-aligned bounding box (AABB) is stored for the subsequent training of an equation detector.

The team will next work on the preprocessing of the extracted TeX tokens to provide the equation decoder a more consistent input. At minimum, the preprocessing will include the removal of superfluous code such as \label{} directives, the normalization of certain latex expressions (e.g., arbitrary ordering of super and sub-scripts in equations), and expanding user-defined macros.

Data driven analysis of preamble to inform template design

The team has conducted an analysis on a sample of 1600 of the arXiv retrieved sources to inform the design of the templates used to render standalone equation images. The purpose of this analysis is the identification of the math environments and TeX packages that are most commonly used for the writing of math in academic papers. By knowing which environments and packages are most common, the team can assemble a template that (a) has broad coverage (i.e., can make the most use of the training data) and (b) is minimal (i.e., will be faster to run and will have fewer conflictes).

The analysis shows that the most commonly used math environments (in order) are: equation, align, and \[ \]. While the team currently handles the equation environment (40% of the equations found), the pipeline will be extended to accomodate the other two as well. In terms of the preamble packages related to math rendering, both amsmath and amssymb occurred in over 70% of the main files, and the next most common package (amsfonts) occurred in only 35% of the main files. Accordingly, the initial template for rendering the standalone equations contains those two most prevalent packages for now, with the option to extend as needed in the future.

Deploying `im2markup` on UofA HPC

The team has also built a singularity container with the lua and Python libraries required to run im2markup. This will allow for rapid development of the equation decoding system.

Model Analysis

A key goal of model analysis is to enable comparison of models that describe the underlying target domain. When the models overlap, they share some variables, but likely not others. The first task in comparing GrFN function networks is to identify where the models overlap. We first review the team’s work on automating function network comparison, and then present some initial results investigating the complexity of running sensitivity analysis, which in turn is informing our next approaches to scaling sensitivity analysis.

Automated function network comparison

During this phase, the team developed an algorithm to identify the shared portion of two function networks. As a working example, we show what the algorithm identifies as the overlapping subnetworks of two evapotranspiration models in the DSSAT system: ASCE and Priestley-Taylor. The following two figures show a graphical representation of the shared portions of these two models, which are identified by a network property that we refer to as a Forward Influence Blanket (FIB). In the following section we will formally define the structure of a FIB and its role in model analysis.

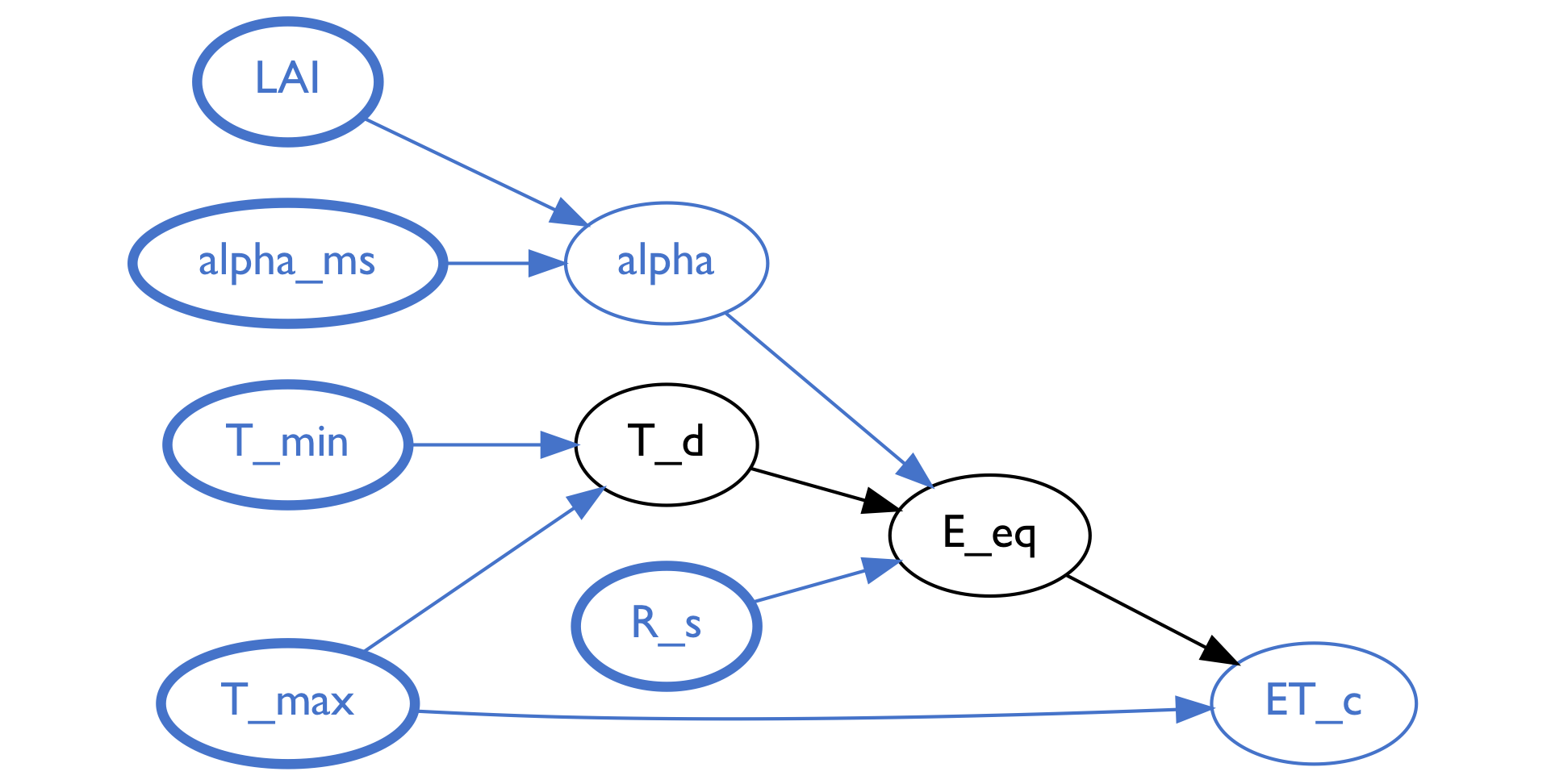
Representation of the subnetwork within the Priestley-Taylor model identified by the Forward Influence Blanket that intersects with the ASCE model

Figure 4: Representation of the subnetwork (blue and black nodes) within the Priestley-Taylor model identified by the Forward Influence Blanket that intersects with the ASCE model.

Representation of the subnetwork within the ASCE model identified by the Forward Influence Blanket that intersects with the Priestley-Taylor model

Figure 5: Representation of the subnetwork (blue and black nodes) within the ASCE model identified by the Forward Influence Blanket (blue and green nodes) that intersects with the Priestley-Taylor model.

Identifying the Forward Influence Blanket (FIB)

Drawing a loose analogy to a Markov Blanket, a Forward Influence Blanket identifies the variables that are shared between two function networks, along with the non-shared variables that are involved in any functional relationships that are along the directed paths between the shared variables. The FIB gets its name because we are analyzing the influence that variables have on one another in a directed (forward from input to output) network, and the blanket identifies minimal subset of such influences shared between the two networks.

The two figures above depict (through node coloring) the portions of the function networks for the two models identified as overlapping. The nodes in the graphs represent variables, the directed arcs indicate directed functional relationships (the variable at the tail is an input, the variable at the head is the output variable that is a function of the input), and the nodes are color-coded to provide a visual depiction of different relationships with respect to the FIB.

Consider the second figure, depicting the ASCE function network. All the blue nodes in the network represent variables that are also found in the Priestly-Taylor model. The blue nodes with thicker lines represent variables that play "input" roles in both of the overlapping subnetworks: they are shared and do not have any parents that are also in the subnetworks.

Next, between the blue nodes and along the directed paths from the "inputs" to the output nodes, are black nodes that represent variables that are not shared between the two models; these indicate intermediate values that may represent differences in the functional relationships between the inputs and outputs of the subnetwork. Determining what the functional differences may be is the subject of the next phase, sensitivity analysis, described in the next section.

In the first figure, depicting the Priestley-Taylor function network, all of the black nodes are between blue nodes. In fact, there are no other nodes or edges that are not colored blue and black. This means the inputs and outputs of the Priestley-Taylor network are "contained within" the ASCE network while there are some differences in the computation between the inputs and outputs (the black nodes).

In the ASCE network, however, there are a number of additional nodes: the green colored nodes identify the variables that have directed influence on the computations along the paths from inputs to outputs, although they are not shared between the networks. If one is interested in directly comparing the subnetworks to each other, the states of the green variables may affect the input-to-output relationships.

Finally, the orange nodes represent all of the variables in the ASCE model that are not shared by the Priestley-Taylor model and cannot directly affect the functional relationships between the shared inputs and outputs without either first passing through a blue or green node. It is in this sense that the green and blue nodes together form the blanket that isolates the functional relationships between the inputs and outputs that are shared between the two networks. If we understand the functional relationships among the blue and green nodes, then we can separately consider how the orange nodes affect each other, and their relationships are only relevant to describing the behavior of the ASCE model. This provides a nice way of factoring the overall analysis into separate analysis tasks.

Having identified the FIB, with the blue and green nodes constituting all of the inputs that can eventually affect the output(s), we can now turn to analyze the functional relationship between inputs and outputs, including the sensitivity of output variables to input variable values.

Sensitivity index discovery

In our previous report we demonstrated the ability to automatically conduct sensitivity analysis on the inputs to an extracted function network. The method we presented involved three steps to fully conduct a sensitivity analysis of a given function f:

Take N samples from the input space of f using Saltelli sampling
Evaluate each of the N samples on f to form the set E
Perform Sobol analysis on E
Recover the $S_1$, $S_2$, and $S_T$ sensitivity indices

This method has been successful in retrieving all the information we needed in order to determine which inputs account for the most uncertainty in model output. Since our last report the team has begun investigating how the runtime of sensitivity analysis is affected by varying the sample size N or the size of the input space (number of input variables) of function f. The purpose of this study is to understand which aspects of models contribute to the complexity of sensitivity analysis. Below we present and discuss plots of runtime as a function of the sample size and number of variables. For each of these graphs the red line shows the runtime for the entirety of sensitivity analysis and the blue line shows the runtime of part (3) of the analysis. All run times are in units of seconds.

Runtime as a function of sample size

As models become more complex we expect that we will need to increase the number of samples taken and evaluated in order to achieve comparable accuracy in sensitivity index estimation during sensitivity analysis. Because of this, we determined that we needed to empirically inspect the runtime of sensitivity analysis as the number of samples increases. From the graph below, we can see that the increase in runtime as the number of samples increases is nearly linear (with slight super-linear trend), both for the entirety of sensitivity analysis and for the Sobol portion of sensitivity analysis. This result is encouraging because it suggests that as long as we maintain only a linear increase in the number of samples required to conduct sensitivity analysis on our larger models then we should not see a runtime increase that would render sensitivity analysis intractable.

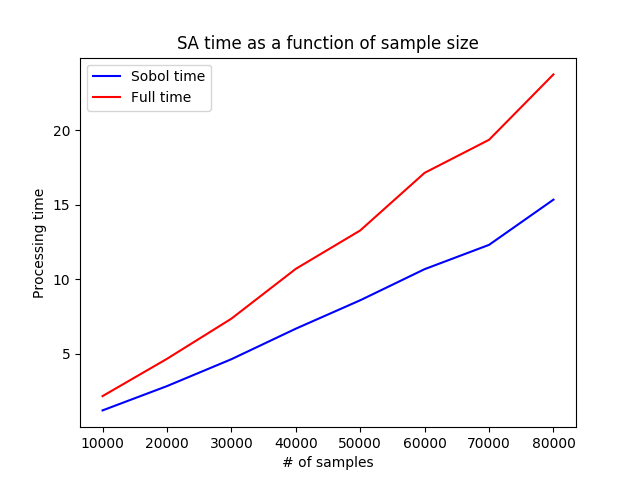
Plot of the increase in runtime for our Sobol
analysis method as sample size increases. The blue line depicts
the increase in runtime for the Sobol algorithm and the red line depicts
the runtime for the total program.

Figure 6: Plot of the increase in runtime (seconds) for our Sobol analysis method as sample size increases. The blue line depicts the increase in runtime for the Sobol algorithm and the red line depicts the runtime for the total program.

Runtime as a function of the number of input variables

We are also exploring the impact of increasing the number of input variables considered during an analysis on overall runtime. As expected, the graph below does show that the runtime for the Sobol portion of sensitivity analysis increases super-linearly as the number of input variables increases. To address this, we are currently exploring several ways to reduce the number of inputs analyzed at one time. One strategy already described above, motivating the FIB analysis, is to identify modular components of the function network with fewer inputs that can be analyzed independently. We are also exploring doing this at the level of performing sensitivity analysis one function at a time, and then composing the results. This work is ongoing.

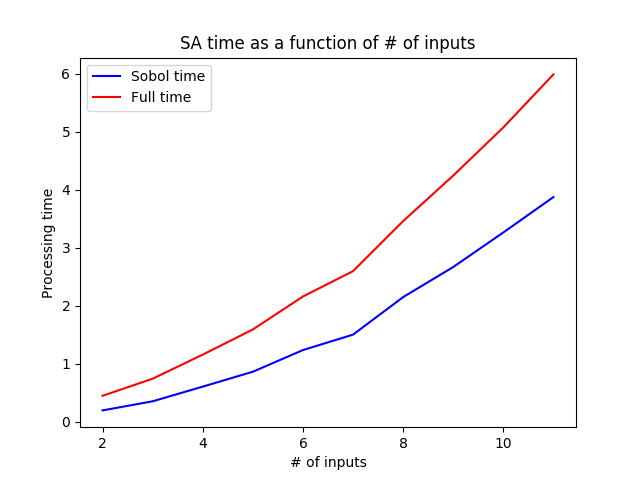
Plot of the increase in runtime for the Sobol analysis
method given an increase in number of inputs for the function under
analysis. The blue line depicts the increase in runtime for the Sobol
algorithm and the red line depicts the runtime for the total
program.

Figure 7: Plot of the increase in runtime (seconds) for the Sobol analysis method given an increase in number of inputs for the function under analysis. The blue line depicts the increase in runtime for the Sobol algorithm and the red line depicts the runtime for the total program.

Code Summarization

During this phase, the team began exploration of an encoder/decoder neural network model for code summarization generation. Initial results demonstrated that the model was not able to acquire enough signal to adequately generate docstring summarizations for source code. In response, the team developed the following three tasks to improve the model.

The first task involved reassessing the quality of the code/docstring training corpus to see if there are avoidable sources of error in the corpus and to attempt to gather more data.
The second task involved trying different approaches to the code/docstring embeddings by investigating the vocabulary size (too may vocabulary items can lead to data sparsity) and possible methods for reducing the vocabulary.
The third task involved creating a model for a simpler task (classification) that has the same form as the model for our generation task but that we can used to directly assess the embedding representation quality.

In the following three sections we will outline the progress we have made on these three tasks.

Progress on code/docstring corpus

The team was able to increase the size of our overall code/docstring corpus by indexing more Python packages to identify additional Python functions that have PEP-style descriptive docstrings. We were able to index additional Python packages from the following lists of packages: the anaconda distribution, the awesome-python list, and the list of all available SciKit packages. In total, we increased the amount of Python packages that we are searching for code/docstring pairs from 24 to 1132.

From these packages, we have extracted code/docstring pairs, increasing our corpus from approximately 22,000 examples to approximately 82,000. The following graphic summarizes the styles of code-bases and their relative contributions to the code/docstring pairs to our corpus.

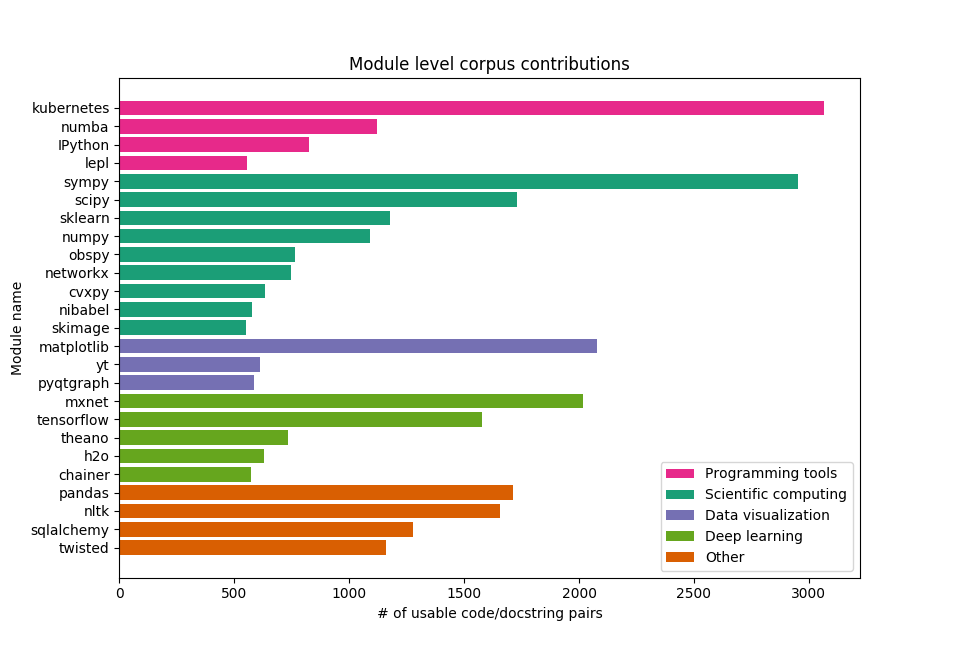
Graphical view of the amount of usable code/docstring
pairs each python module has added to our code-summarization corpus
(only the 25 modules with the largest amount of usable pairs are shown)
Modules are color-coded according to the type of code most likely to be
found in the module.

Figure 8: Graphical view of the amount of usable code/docstring pairs each python module has added to our code-summarization corpus (only the 25 modules with the largest amount of usable pairs are shown) Modules are color-coded according to the type of code most likely to be found in the module.

Progress on code embeddings

Neural network model performance has been found to strongly depend on the quality of the embedding model used to represent the data. One of the biggest struggles for any embedding is to ensure that enough examples are present for every token you wish to embed. Without a large number of examples the embedding space cannot create meaningful embeddings for corresponding tokens. In the case of creating embeddings for code, it is likely the case that the names of functions are going to be some of the most important tokens to embed, and unfortunately these are also the most infrequent if each unique name is treated as a single token. From our original dataset of 22,000 examples we had roughly 53,000 unique tokens in the code portion of our corpus. The vast majority of these were function or variable names that occurred fewer than five times each, not nearly enough to be able to establish useful embeddings that capture the type of semantic information carried in function or variable names.

To address this issue, we split function and variable names into sub-components using snake_case and camelCase rules, to extract the repeated mentions of name that occur as parts of function and variable names. Some examples of the tokenized forms of function names found in our corpus before and after the transformation are provided in the following table.

Original tokenization	Split-name tokenization
`compute_ldap_message_size`	`<BoN> compute ldap message size <EoN>`
`getComponentByPosition`	`<BoN> get Component By Position <EoN>`
`fromOpenSSLCipherString`	`<BoN> from Open SSL Cipher String <EoN>`
`fromISO8601`	`<BoN> from ISO 8601 <EoN>`

Splitting functions/variable names in this way decreased our code vocabulary size from roughly 53,000 to roughly 16,000 unique tokens while also lowering the number of tokens that appear fewer than five times from roughly 35,000 to roughly 5,000.

Docstring classification task

One of the difficulties with generation tasks is being able to tell whether your model has enough signal from the data to be able to generate affectively.

In order to evaluate whether our dataset provides enough signal for our generation task, we have designed a separate classification task in which the classifier is presented with a code and docstring pair and must predict whether the docstring describes the code, which we approximate by using the docstrings associated with code blocks in our corpus. In the following sections we describe the the classifier, present the two classification datasets we are using, present some preliminary classification results, and discuss the next steps for using these methods to improve the code summary generation model.

Baseline neural model description

Our initial classification model is a simplification from the model we originally planned to use for generation. The model first embeds a code sequence using our pretrained code embeddings and embeds a docstring using our pretrained docstring embeddings. The two embedded sequences are each fed into their own respective Bi-LSTM recurrent network. The final hidden state outputs from these networks are then concatenated and fed into a deep feed-forward neural network that produces a binary classification of whether the docstring is correctly paired with the provided function.

Our rationale for simplifying the model used for classification is that we are currently testing to see if our data is providing enough signal to aid in classification. Once we verify that we do have enough signal to allow for decent classification results, we will increase the models complexity. It is important to note that since the main purpose of the classification model is to test the fitness of our data for generation, we cannot add any docstring specific information to the classification model, since such information would not be present during docstring generation.

Random-draw and challenge dataset description

We have constructed two different datasets from our code/docstring corpus that we will use to test the classification model. The corpus itself only provides positive examples of docstrings paired with code blocks, so in order to create negative examples, we use a common practice in NLP known as negative sampling to match code blocks with docstrings other than their correct docstring. This creates instances for our classifier to correctly label as mismatched pairs. We have done this with both of our datasets.

For our first dataset, we use uniform random sampling to select our negative examples. We named this the “random-draw” dataset. We anticipate that this dataset will be easier to obtain good performance as uniform random sampling is likely to pair docstrings with code that is completely unrelated. This dataset is used for the earliest phases of experimentation with our classifier as we are expected to have better chance of training success. Once we determine that our classifier can do reasonably well on the random-draw dataset we will move on to testing our model on our second dataset.

The second dataset uses lexical overlap between the true docstring for a code block and the other candidate docstrings to select a candidate that has the highest lexical overlap with the true docstring (i.e., shares many of the same terms), but is not the correct pairing. This is called the “challenge” dataset, as now the “mismatch” pairings are much more likely to be close but still not correct. This allows us to rigorously test our classifier’s ability to correctly identify whether a code/docstring pair is mismatched. To build the dataset, we use Apache lucene to index and query our set of docstrings. The following table shows five docstrings with their negative example docstring of highest lexical overlap is provided in the table below.

Module paths (source, negative)	Source docstring	Best negative example
`kubernetes.client.api` `tabpy.client.rest`	Builds a JSON POST object	Issues a POST request to the URL with the data specified . Returns an object that is parsed from the response JSON
`sympy.ntheory.multinomial` `statsmodels.iolib.table`	Return a list of binomial coefficients as rows of the Pascal’s triangle	Return list of Row , the raw data as rows of cells
`matplotlib.image` `PIL.image`	Set the grid for the pixel centers , and the pixel values	Gets the the minimum and maximum pixel values for each band in the image
`mxnet.model` `tensorflow.engine.training`	Run the model given an input and calculate the score as assessed by an evaluation metric	Sets the metric attributes on the model for the given output
`twisted.internet.tcp` `gevent.server`	Create and bind my socket , and begin listening on it	A shortcut to create a TCP socket , bind it and put it into listening state

Initial classification results

We have trained and evaluated our baseline model on the random-draw dataset that was generated by our original corpus (22,000 pairs). After processing over our training set for 35 epochs, our validation set accuracy was 80%, a result that we are very excited about!

Next steps

Now that we have increased our corpus size and created our challenge dataset, our immediate next task is to re-evaluate our baseline model on both the random-draw dataset and challenge dataset to see how the changes to our code/docstring corpus affect our performance on our two datasets.

Pending encouraging results on the above experiments, we will begin increasing the complexity of the model by adding character embeddings for the code/docstring tokens. We also plan to add attention layers to the LSTM output from the code and docstring LSTMs that add attention on the alternate sequence respectively. If the results from the above experiments are not as good as we hoped then we will also investigate adding more docstring data to our docstring embeddings from large online documenation repositories such as ReadtheDocs to improve the signal from our docstring sequences.

AutoMATES